GT maths-bio 2013
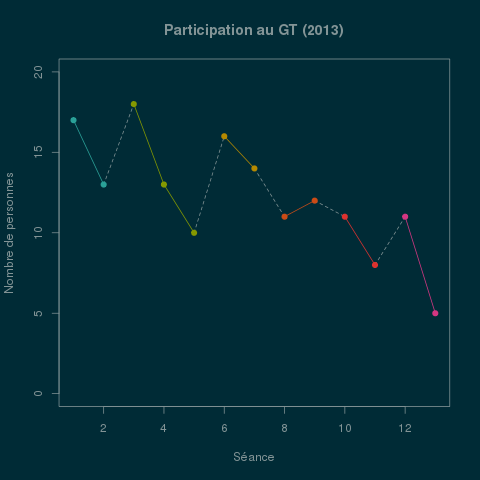
Séances
Théorie des jeux
La théorie des jeux formalise la notion de jeu, permettant ainsi d'étudier les propriétés de différentes stratégies dont le but est de maximiser un gain. Créée au XXème siècle en lien direct avec des problèmes d'économie, plusieurs éléments font que, sous sa forme la plus simple — qui considère des joueurs parfaitement rationnels et disposant de toute l'information dont ils ont besoin —, ses applications en économie ne sont pas toujours très pertinentes...
En revanche, ces hypothèses sont tout à fait pertinentes en évolution où l'on s'attend à ce que toute stratégie non-efficace soit contre-sélectionnée, avec pour conséquence que les stratégies adoptées par les organismes sont celles qu'auraient adoptées des joueurs rationnels.
Au cours de deux séances, nous avons introduit la théorie des jeux, et en avons montré quelques applications en évolution. Nous avons étudié en détail, grâce à quelques rudiments de théorie des systèmes dynamiques, quelques jeux évolutifs classiques comme le jeu Faucon-Colombe et plusieurs de ses variantes.
Modèles matriciels de populations
Les modèles matriciels de populations sont parmi les modèles de dynamique de populations structurées les plus simples : ils permettent de suivre la dynamique en temps discret d'une population au moyen de produit matriciels répétés. Loin d'être un problème, cette simplicité en fait justement un outil de choix pour attaquer certaines questions de façon purement analytique. Elle rend également l'utilisation de ces modèles relativement simple à mettre en oeuvre, expliquant leur grande importance en biologie de la conservation. Les modèles matriciels de population sont donc une base indispensable pour quiconque s'intéresse à l'écologie des populations ou à la conservation.
Aux cours des trois séances qui leur ont été consacrées, nous avons surtout étudié les propriétés générales de ces modèles, sans développer de résultats liés au cas particulier des modèles de Leslie (modèles en classes d'âge). Nous nous sommes concentrés sur la construction et l'interprétation du modèle, la primitivité et le théorème de Perron-Frobenius. La dernière séance a été consacrée à une réflexion en groupe sur le temps de génération.
Des notes sur les modèles matriciels de population sont disponibles en pdf au format A4 et au format liseuse.
Analyse en groupement
L'analyse en groupement (cluster analysis en anglais) est un domaine à l'interface entre mathématiques (essentiellement par les statistiques) et informatique (essentiellement par l'intelligence artificielle) qui s'intéresse à l'apprentissage automatique non supervisé. On entend par là le développement de méthodes automatisables permettant le partitionnement d'un jeu de données en un certain nombre de sous-ensembles partageant des propriétés communes : il s’agit de mettre en évidence sa structure sous-jacente. À l'heure de la multiplication et de l'accroissement en taille des jeux de données (séquences, profils d'expressions, inventaires, suivis GPS) la capacité à déceler des régularités dans un ensemble d'observations devient de plus en plus cruciale en biologie moderne.
Au cours de ces deux séances d'introduction à l'analyse en groupement nous avons abordé la notion de similarité, c'est à dire la formalisation de la la notion intuitive de "deux objets se ressemblent-ils beaucoup ou pas ?". Ensuite, nous avons décrit les principes de quelques grandes familles d'algorithmes de classification non supervisée et nous avons terminé par la question de l'évaluation d'un partitionnement de données.
Des notes sur l'analyse en groupement sont disponibles en pdf au format A4 et au format liseuse.
Remarque : ce sujet ayant précédé celui sur l'apprentissage et les chaînes de Markov cachées, dont la première partie a consisté à établir un cadre général à l'apprentissage et dont la seconde a repris en détail certains concepts abordés lors des séances sur l'analyse en groupement, les deux sujets gagnent sans doute à être lus ensemble.
Apprentissage et chaînes de Markov cachées
L'utilisation de modèles mathématiques est, particulièrement en biologie, primordiale pour expliquer et prévoir des phénomènes. Mais, une fois un modèle établi, une question essentielle se pose : comment, en jouant sur les paramètres, adapter ce modèle afin qu'il puisse s'harmoniser le plus finement possible avec les observations ? Répondre à cette question est l'objet d'une branche à part entière des mathématiques appliquées mêlant analyse et optimisation, probabilités et statistique, et algorithmique.
Dans le cadre du GT, nous avons d'abord posé un cadre général pour l'étude de ce genre de problème. Nous l'avons ensuite utilisé pour étudier des cas simples et classiques, aussi bien pour des modèles déterministes que pour des modèles probabilistes. Nous nous sommes ensuite focalisés sur l'apprentissage des paramètres de modèles à chaîne de Markov cachées, en établissant l'algorithme Expectation-Maximisation pour un tel modèle. Malheureusement, nous n'avons pas eu le temps d'aborder l'algorithme de Viterbi.
Des notes de la séance d'introduction à l'apprentissage sont disponibles en pdf au format A4 et au format liseuse. Des notes sur les chaînes de Markov seront disponibles très bientôt (mise à jour: février 2015).
Remarque : ce sujet reprenant certains concepts ayant été présentés lors des séances sur l'analyse en groupement (notion de distance, etc...) et fournissant un cadre général à l'apprentissage, les deux sujets gagnent sans doute à être lus ensemble.
Fractales et analyse spatiale
Fractales
Lorsqu'il s'est demandé quelle était la longueur de la côte de Bretagne, Benoît Mandelbrot ne se doutait sans doute pas qu'il était sur le point de créer une branche déroutante des mathématiques : les fractales. Les fractales sont ces objets de surface nulle mais qui remplissent le plan, ces surfaces qui remplissent l'espace, ces formes géométriques des périmètre infini mais de volume fini.
Aussi théoriques que ces objets puissent paraître (il existe tout un champ des mathématiques/de l'informatique qui se demande comment tracer des fractales en pratique), les fractales se révèlent un outil, certes complexe, mais particulièrement puissant pour caractériser de nombreux phénomènes du monde réel, y compris en biologie. Parmi ceux-ci, on peut citer l'organisation de certains objets biologiques qui tirent parti d'architectures modélisables par des fractales (poumon, chou romanesco, ramifications des arbres, organisation de la chromatine dans un noyau eucaryote et propriétés de diffusion des molécules partageant le même volume, etc.)
Après avoir décrit quelques propriétés des fractales (auto-similarité, méthode de construction, "space-filling"), nous avons discuté des apports de ces objets abstraits pour décrire des objets biologiques, et des contraintes se posant à leur application. Nous avons terminé en esquissant la notion de dimension fractale, un nombre qui étend la dimension topologique (1D, 2D, 3D, etc.) à des nombres réels, concept crucial à la base même de la notion de fractale.
Analyse spatiale
Bientôt disponible, avec des notes !
Théorie des graphes
La théorie des graphes : des techniques pour régler tous vos problèmes à base de dessins en bâtons, flèches et points ! Les graphes sont utilisés dans des domaines divers de la biologie pour représenter de très nombreux systèmes : réseaux de gènes, réseaux de neurones, réseaux trophiques, réseau métaboliques...
Une première séance de définitions générales, d'axiomes, et de quelques notions de connexité. Pour la seconde séance, nous sommes partis de la connexité pour partir vers les problèmes de coloration. La coloration est une notion de la théorie des graphes qui peut être utilisée pour représenter les contraintes sur un système. Par exemple, lorsqu'on veut colorier une carte, une contrainte est que deux pays côté à côte ne soient pas coloriés de la même manière (sinon, on ne pourrait pas les distinguer). Nous avons démontré que 5 crayons de couleurs étaient suffisants pour colorier n'importe quelle carte (en réalité, 4 suffisent mais c'est l'objet du célèbre théorème des 4 couleurs, beaucoup plus difficile à démontrer).
Divers
Statistiques
Remerciements
- Farouk Boucekkine, pour avoir mis en place le GT.
- Le département de biologie de l'École normale supérieure, pour
le prêt de ses locaux (et plus particulièrement Anne Zalmanski pour
son aide avec la réservation des salles).
- Benjamin Nguyen-Van-Yen, François Bienvenu, Guilhem
Doulcier, Alexis Jacq, Maxime Woringer et Guillaume
Jeanne, pour avoir animé des séances.
- François Bienvenu et Guilhem Doulcier,
pour avoir tapé et/ou relu des notes sur
certaines séances.