GT maths-bio 2014
![]() Année précédente
Année suivante
Année précédente
Année suivante
![]()
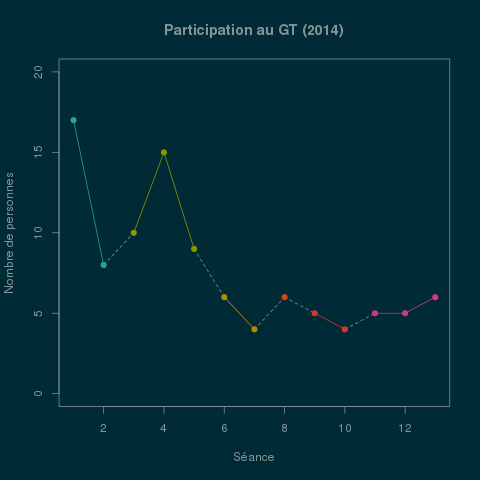
Séances
Théorie des jeux
La théorie des jeux est un domaine des mathématiques très actif (5 prix Nobel depuis 1994, dont un en 2014) qui connaît de nombreuses applications, aussi bien en économie qu'en biologie. Elle regroupe des outils mathématiques très divers dans le but d'étudier les interactions entre plusieurs acteurs qui cherchent à maximiser des intérêts pouvant être contraires.
En biologie, la théorie des jeux a une place centrale dans l'étude de l'évolution. L'accent est alors généralement mis sur les jeux matriciels non-coopératifs. Mais il ne s'agit que d'une petite partie d'une théorie extrêmement vaste ! C'est pourquoi, au cours des deux séances qui lui ont été consacrées, l'accent a été mis sur la diversité des questions étudiées par la théorie des jeux. Au moyen de nombreux exemples, nous avons abordé les principales caractéristiques des jeux : coopératifs vs non coopératifs, symétriques vs asymétriques, répétés vs non répétés, séquentiels vs simultanés, etc. Des notions centrales comme celle d'équilibre de Nash ont également été abordées.
Dans le cadre des séances sur la théorie des jeux, un tournoi de dilemme de prisonnier a été organisé. Ce tournoi a été rendu possible par l'efficacité de Guilhem Doulcier, qui implémenté le code nécessaire à l'organisation du tournoi sans perdre de temps. Le code est disponible ici, et les résultats du tournoi se trouvent sur cette page.
Théorie des groupes
Quel est le lien entre les racine d'un polynôme, les symétries d'un polygone réguliers et la séquence des leviers que Link doit activer pour ouvrir une série de portes ? C'est ce que nous avons essayé de découvrir au cours des trois séances consacrées à la théorie des groupes.
Plutôt que de prendre comme point de départ les axiomes de la théorie, nous avons manipulé un certain nombre d'objets qui nous ont conduit à les introduire de façon naturelle. Nous avons ensuite vérifié que ces axiomes étaient compatibles avec les propriétés que nous avions observées. Enfin, nous avons vu que les groupes pouvaient être utilisés pour caractériser (et ainsi mieux comprendre) certains objets.
Diffusion(s)
La diffusion est étudiée en prépa BCPST. On y voit alors qu'une des principales caractéristiques des phénomènes diffusifs est que "l'espace est exploré en racine de t" au sens que, si Dt est la distance à laquelle une particule diffusive se trouve de son point de départ au temps t, alors E(Dt2) = t. Cela permet, par exemple, de distinguer un transport diffusif d'un transport balistique (où E(Dt2) = t2).
Néanmoins, dans certaines situations (comme dans le cas de protéines diffusant dans une cellule), on observe que E(Dt2) = tα, où α ≠ 1/2. Comment expliquer cela ?
En nous basant principalement sur des simulations, nous avons vu que la réponse pouvait venir de la géométrie de l'espace dans lequel la diffusion se fait...
Méthode des moments
Les moments étant centraux en mathématiques, plusieurs méthodes portent le nom de "méthode des moments". Ici, on fait référence à une méthode introduite en maths-bio dans le début des années 90 pour étudier des systèmes spatialisés. Cette méthode est souvent appelée "pair approximation".
Au cours de la séance, nous avons commencé par motiver l'étude de systèmes spatialisés par un problème tiré de l'écologie-évolution : l'évolution de l'altruisme en population visqueuse. Cet exemple nous a permis de voir les limites des approches classiques (modèles en patches, EDP type réaction-diffusion, automates cellulaires, simulations individus-centrées) et l'intérêt d'une modélisation par des processus ponctuels. Nous avons ensuite présenté la méthode de façon assez générale, en mentionnant au passage un certain nombre d'outils centraux en modélisation (master equations, distributions, statistiques spatiales, fermetures de moments...) en guise de teaser... Pour terminer, nous avons appliqué notre méthode à un système simple et nous avons vu comment une fermeture de moments d'ordre un permet de retrouver le modèle de croissance logistique (et plus généralement les systèmes de Lotka-Volterra).
Des notes sur la méthode des moments pour les processus ponctuels seront disponibles début 2015.
Transformée de Laplace
La transformée de Laplace, qui généralise la transformée de Fourier, est un outil indispensable des mathématiques appliquées. En effet, passer une fonction dans le domaine de Laplace peut simplifier les manipulations et faciliter entre autres la résolution d'équations différentielles. C'est également un outil d'intérêt pour la modélisation de systèmes, et qu'on retrouve en probabilités lorsqu'on en vient à la fonction génératrice des moments d'une variable aléatoire (transformée de Laplace de la densité).
Après avoir repris les notions de convolution avec une orientation système physique, nous avons introduit la transformation de Laplace, qui transforme les produits de convolution en produit. De là, nous avons trouvé des propriétés de cette transformée, notamment la simplification de la dérivation et du décalage temporel. Avec très peu de calculs, nous avons trouvé les transformées de fonctions élémentaires, ce qui nous a permis de résoudre facilement une équation différentielle. Dans une seconde partie, nous avons vu le pendant discret de la transformée de Laplace : la transformée en Z. Résolution d'équations de récurrence, puis application aux probabilités discrètes et continues.
Des notes sur la transformée de Laplace sont disponibles en pdf au format A4 et au format liseuse.
Introduction à la topologie
En mathématiques, et y compris en mathématiques appliquées, on est très souvent amenés à raisonner sur des espaces fonctionnels — c'est-à-dire à manipuler des "fonctions de fonctions". Il est donc important de pouvoir généraliser certains concepts centraux de l'analyse réelle (comme la convergence ou la continuité) à ces fonctions. Cela nécessite de munir l'espace d'une structure appropriée appelée topologie. Le but de ces séances a été d'introduire cette structure de façon aussi naturelle que possible, puis d'en étudier quelques propriétés — sans toutefois perdre de vue nos objectifs initiaux.
Nous avons donc commencé par introduire la notion de distance, à partir de laquelle nous avons muni l'espace d'une structure permettant de généraliser des notions comme la convergence ou la continuité. Mais, après avoir manipulé un peu cette structure, nous nous sommes rendu compte qu'on pouvait souvent se passer de la notion de distance. Cela nous a conduit à définir la notion de topologie. Enfin, nous avons terminé autour de deux notions importantes : la complétude et la compacité, dont nous avons illustré l'intérêt par le théorème du point fixe de Picard et le théorème des bornes atteintes.
Une des ambitions principales de ces séances était d'introduire un vocabulaire et des notions de base (ouverts, fermés, convergence, continuité, densité, complétude, compacité...) indispensables à la lecture d'articles de biologie mathématique.
Des notes d'introduction à la topologie sont disponibles en pdf au format A4 et au format liseuse.
Divers
Statistiques
Remerciements
- Le département de biologie de l'École normale supérieure, pour
le prêt de ses locaux et l'hébergement de ce site (et plus particulièrement
Anne Zalmanski et Pierre Vincens).
- Gaëtan Fournier, Farouk Boucekkine,
Maxime Woringer, François Bienvenu et
Guillaume Jeanne, pour avoir animé des séances.
- Félix Foutel-Rodier et François Bienvenu,
pour avoir tapé et/ou relu des notes sur
certaines séances.
- Guilhem Doulcier, pour son implémentation dans l'urgence d'un programme ayant rendu possible le tournoi de dilemme du prisonnier, ainsi que Guilhem Doulcier (décidément !), François Bienvenu et Marc Oudart, pour avoir soumis des stratégies lors du tournoi.