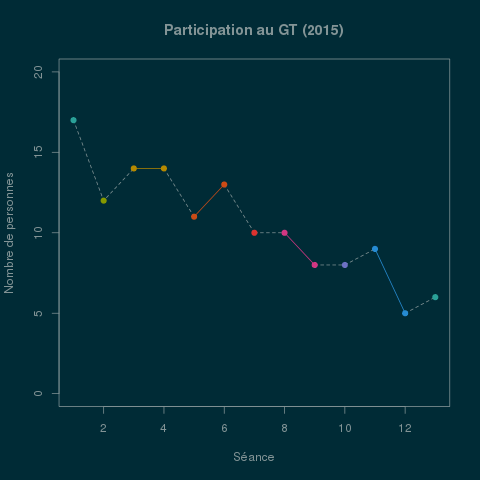
GT maths-bio 2015
![]() Année précédente
Année suivante
Année précédente
Année suivante
![]()
Séances
Autour des suites
Les cas dans lesquels le nème terme d'une suite peut être explicitement calculé ne sont pas légion. Donner un nom à une suite définie par récurrence, comme « factorielle n », ne constitue pas une avancée : « factorielle n » ne peut a priori être calculé que par récurrence en multipliant n et factorielle (n - 1). Pour trouver un ordre de grandeur de factorielle 245, il faut passer par la notion d'équivalent d'une suite. Une autre motivation est l'équivalent du nème nombre premier qui constitue, historiquement, un des plus beaux accomplissements des mathématiques.
Pour analyser ces questions, la séance s'est articulée autour des rappels sur les définitions rigoureuses (de convergence) permettant de définir la notion d'équivalence de deux suites, c'est-à-dire grosso modo lorsque leur quotient tend vers un. De manière peut-être étonnante, un moyen standard et très puissant de trouver des équivalents de suites est de passer par la série télescopique associée. Cette idée a motivé un détour par quelques résultats de base sur les séries à termes positifs.
Fort de ces outils, le reste de la séance a été consacré à établir un équivalent pour factorielle (formule de Stirling), et pour une suite récurrente non classique, les séries étant à chaque fois décisives.
Algorithmes sur les graphes
Les graphes sont des objets mathématiques qui peuvent être utilisés pour représenter des interactions. Ils sont donc très présents en biologie, où on les retrouve pour représenter des réseaux métaboliques ou de régulation de gènes, des chaînes trophiques ou encore des structures de population.
Dans cette séance nous avons abordé quelques notions de base de la théorie des graphes avec pour objectif de démontrer l'algorithme de Kruskal. Cet algorithme permet de trouver un arbre recouvrant de poids minimum, c'est-à-dire de minimiser un coût attribué aux connexions d'un graphe tout en maintenant le graphe connecté. Nous avons naturellement été amenés à parler d'arbres, à les définir et à les caractériser.
Équations différentielles
coming soon...
Introduction à l'intégration
Intégrer consiste à calculer des "volumes" en sommant des petits volumes élémentaires. Cette opération qui peut sembler peu passionnante se révèle en fait être au coeur de nombreuses branches diverses des mathématiques et de la physique, en partie du fait du lien entre intégration et calcul de primitives. Ainsi, la théorie de l'intégration a une place centrale en mathématiques – et notamment en mathématiques appliquées, car elle sous-tend la théorie des probabilité ainsi qu'une grande partie de l'analyse fonctionnelle.
Plutôt que de commencer directement par la version moderne de l'intégration, nous avons adopté une démarche "historique" en commençant par effectuer quelques rappels sur l'intégrale de Riemann, avant d'en montrer les limitations. Contourner ces limitations nous a conduit à construire l'intégrale de Lebesgue, dont nous avons ensuite étudié les principales propriétés.
Arbres discrets pour la biologie évolutive
Les arbres sont des objets omniprésents en biologie, et particulièrement en biologie évolutive, où ils sont utilisés pour représenter les relations de parenté entre séquences biologiques, entre individus, ou encore entre espèces. Entre les schémas de coin de cahier dessinés par Darwin au XIXème siècle et l'explosion du nombre et de la taille des phylogénies reconstruites pour des organismes très divers à laquelle on assiste aujourd'hui, la biologie évolutive théorique a réalisé un bon de géant. En particulier, elle a dû se doter d'un formalisme mathématique permettant de décrire, modéliser et analyser les arbres.
Cette séance de 2h est l'occasion de s'intéresser à ce formalisme. On part de la description d'un arbre comme un graphe particulier, avant de s'intéresser à deux descriptions ensemblistes (les hiérarchies et les splits), qui permettent entre autres de comparer plusieurs arbres ou de créer un arbre consensus facilement. On finit, enfin, par la représentation de caractères discrets sur nos arbres. Quelques petits problèmes de dénombrement sont abordés tout au long de la séance pour permettre de manipuler les différentes notions.
Les notes sur les arbres de Marc Manceau sont disponibles format A4 et au format liseuse.
Optimisation
Les problèmes d'optimisation – qui consistent simplement à trouver les extremas de fonctions de plusieurs variables – se retrouvent dans de très nombreux situations. Par exemple, on peut chercher à trouver la droite qui "approche le mieux" un ensemble de points : en définissant une fonction qui à un couple (coefficient directeur, ordonnée à l'origine) associe une valeur d'écart aux données, on cherche alors à trouver le couple qui minimise cette fonction d'écart. Une fois formulés sous forme d'optimisation, les problèmes peuvent être résolus de manière efficace par des méthodes et des algorithmes bien étudiés, comme la descente du gradient.
La première séance a porté sur la formulation de problèmes classiques (régression, problèmes de ressources, etc), sans contrainte dans un premier temps, puis avec des contraintes sur les paramètres à optimiser. L'équivalence entre les deux familles de problèmes est finalement apparue par l'introduction de pénalités, puis des multiplicateurs de Lagrange et de Karush-Kuhn-Tucker. La résolution de ces problèmes à petite dimension peut se faire par méthode de descente du gradient, dont nous avons expliqué le principe général. Des méthodes cousines, aussi efficace en cas de fonctions régulières ou pour lesquelles les gradients et matrices hessiennes sont faciles à calculés, ont également été abordées.
La seconde séance a passé en revue les concepts de l'optimisation discrète et notamment la régression logistique et les réseaux de neurones. A l'aide d'un programme écrit en Python, nous avons pu développer un exemple pendant toute la séance. La courbe en S a été analysée sous tous les angles et nous avons vu son application aux réseaux de neurones.
La niche écologique
La niche écologique d'une espèce est généralement définie comme la caractérisation de son habitat au sens large (physico-chimique, mais aussi biologique). Il s'agit de la pierre angulaire de l'écologie des communautés et elle peut être formalisée mathématiquement de différentes façons :
- L'approche démographique de la théorie moderne de la coexistence fait
le lien entre les équations différentielles de la dynamique des
populations le principe d'exclusion compétitive.
- L'approche en réseaux utilisant les graphes d'interactions entre
espèces (réseaux trophiques, interactions plantes pollinisateurs), très
riches en information sur la structure des communautés, permet plusieurs
définitions de la niche écologique.
- L'approche statistique consistant à reconstruire l'enveloppe des
espèces dans un espace de trait multidimensionnel permet une étude
quantitative de niche écologiques complexes fondées sur une observation
directe des traits des individus.
Cette séance a été consacrée à la présentation de ces différentes approches.
Théorèmes limites en probabilités
Lors que l'on jette un dé un grand nombre de fois, il est intuitif que la proportion de "un" obtenus va tendre vers 1/6. Ceci traduit le fait que répéter une expérience de façon indépendante permet d'obtenir des propriétés de convergence de quantités calculées à partir de la suite des expérience, comme la moyenne.
Le but de cette séance a été de présenter différents théorèmes permettant de quantifier ces convergences (lois des grands nombres, théorème central limite, théorème de Berry-Essen). L'accent a été mis sur le fait qu'on peut en quelque sorte voir ces théorèmes comme fournissant des "développement limités" de la moyenne, dont les coefficients correspondent au moments de la variable aléatoire que l'ont répète identiquement et de façon indépendante.
Divers
Statistiques
Remerciements
- Le département de biologie de l'École normale supérieure, pour
le prêt de ses locaux et l'hébergement de ce site.
- Camille Pouchol, Félix Foutel–Rodier,
François Bienvenu, Marc Manceau, Guillaume Jeanne,
Simon Jégou, Guilhem Doulcier et François Stransky,
pour avoir animé des séances.
- Marc Manceau, pour avoir tapé des
notes.